Burc Karakas · 19 Şubat 2021

Yazılım ve bilgisayar mühendisliği başta olmak üzere, algoritmalar konusunda eğitim gören her öğrenci hayatında en az bir kez "Hanoi Kuleleri" adlı bir algoritma ismi duyar. Bu algoritma, kimi zaman ödev olarak, kimi zamansa kocaman bir ders olarak karşımıza gelir çünkü gerçek bir yapı taşıdır.
Hanoyi uzak doğuda Vietnam sınırları içerisinde bulunan bir şehir olmakla birlikte kendine has mimariye sahip kuleleriyle de ünlü bir başkenttir. Şehir ve mimarisi nasıl bir algoritmaya dönüştü derseniz;
Bu sorun, 1883 yılında Fransız asıllı matematikçi Edouard Lucas tarafından bulunmuş ve oyuncak olarak satışa sunulmuştur. Oyuncağı edinen çocuklar, 3 tane dikine çubuk (kule) ve 8 tane de disk ile karşılaşır. Problemimize göre ise; 1. kuleye diskler boy sırasına göre küçükten büyüğe doğru her seferinde bir diski hareket ettirmek ve bir diski asla kendinden ebat olarak küçük bir diskin üzerine koymamak şartıyla kulede yer alan diskleri diğer iki boş kuleye en az kaç hamlede aktarabiliriz? Sorusunun cevabını aramaktayız.
Bu karmaşık sorunun cevabı için belli tanımlamalar yapmamız gerekir.
Çözümü ise;
Kulede bulunan disk sayısını n olarak kabul edip, en az 2n-1 kadar hamle gerektiğini fark ederiz. Böylece 3 disk 7, 4 disk 15, 5 disk ise 31 hamlede aktarılmış olur. Bu sayıların mantıklı takibi ise 8 disk için 2⁸-1=256–1=255 cevabını bize verir.
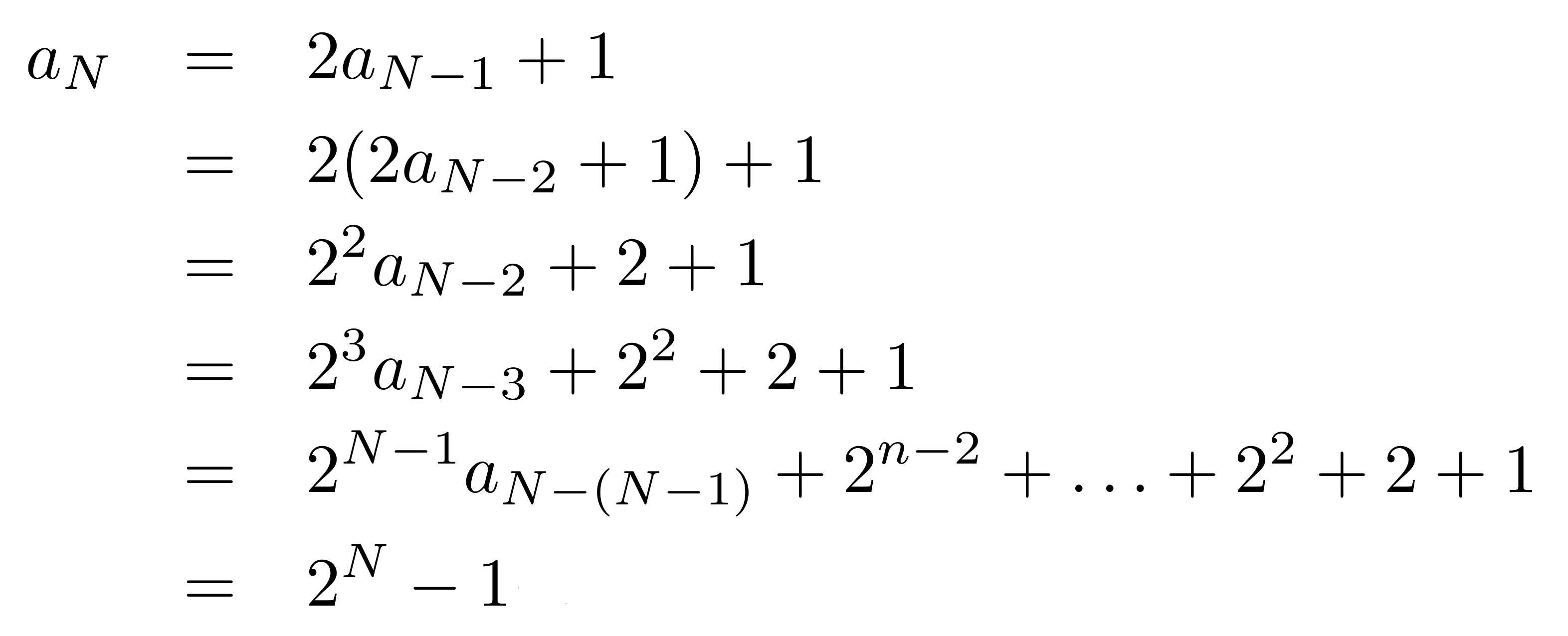
Hanoi Kulelerinin bir zorlu rakibi daha vardır ki o da Hindistan'ın Benares şehrinde bulunan bir tapınakta yer alan Brahma Kulesi'dir. Çünkü Brahma Kulesi'nde 64 adet altın disk bulunur ve tapınakta yaşayan rahipler nesillerdir bu 64 diski boş iki çubuğa aktarmanın yolunu arıyor.
Hanoi örneğinde verdiğimiz formülü buraya entegre ettiğimizde ise 2n-1'den takriben 20 basamaklı bir sayı elde edilir ki rahipler için saniye başına bir disk aktarımı söz konusu olsa dahi milyarlarca yıl sürecek bir iş anlamına gelir.

 Geri
GeriHayalinizdeki üniversiteyi bulalım